C++ Компьютерная графика

Построить изображение поверхности z=f(x,y) в параллельной проекции ex = y – 0.7 x, ey = z – 0.7 x.

Задание
Разработать программу на языке программирования Borland C++  Builder для вывода на экран изображения поверхности с удалением невидимых линий.
Введение
В данной работе отражен вывод на экран изображения поверхности в среде программирования Borland С++ Builder 6 Enterprise.

Построить изображение поверхности

z=f(x,y)

в параллельной проекции

ex=y-0,7x

,

ey=z-0,7x

.

//---------------------------------------------------------------------------
#include <vcl.h>
#pragma hdrstop
#include <math.h>
#include "rgz03.h"
//---------------------------------------------------------------------------
#pragma package(smart_init)
#pragma resource "*.dfm"
TForm1 *Form1;
#include <stdlib.h>
#include <math.h>
#define nx 100
#define ny 100

int algor=1;
float xmax = 3, xmin = -3, ymax = 3, ymin = -3,  zmax = 3, zmin = -2,hx,hy;
float xv = 50, yv = 30.5 , zv = 10 ; // положение наблюдателя
float d = 1,zz=0.2 ;            // расстояние до плоскости проекции
float cosa, sina ;         // меридиана точки наблюдения
float exmax, exmin, eymax, eymin ;
int gmex, gmey ;
int *phimin, *phimax ;
float cvals[ny+1], cval ;

void line(int x0, int y0, int x1, int y1){
        Form1->Image1->Canvas->MoveTo(x0,y0);
        Form1->Image1->Canvas->LineTo(x1,y1);
}

void sline( int x0, int y0, int x1, int y1 ){
int i,j, temp, x, y, maxacc, accx, accy, dx, dy,
            length=abs(x1-x0);
     if ((i=abs(y1-y0))>length) length=i;
//     if (length==0) return;
     maxacc=2*length; accx=accy=length;
    for (j=0; j<2; j++){
      dx=2*(x1-x0); dy=2*(y1-y0); x=x0; y=y0;
        length+=j;
      for (i=0; i<length; i++){
                              if (y0<=y1&&phimax[x]<y){
                        Form1->Image1->Canvas->Pixels[x][gmey-y]=clBlack;
                        phimax[x]=y;
            }
            if (y0>=y1&&phimin[x]>y){
                        Form1->Image1->Canvas->Pixels[x][gmey-y]=clBlack;
                        phimin[x]=y;
            }
            accx+=dx; accy+=dy;
            if (accx>=maxacc){
                accx-=maxacc; x++;
            } else if (accx<0){
                  accx+=maxacc; x--;
              }
            if (accy>=maxacc){
                  accy-=maxacc; y++;
            } else if (accy<0){
                  accy+=maxacc; y--;
              }
      }
      temp=x0; x0=x1; x1=temp; temp=y0; y0=y1; y1=temp;
     }
}

float fz(float x, float y) {return ((x*y)/(x*x+y*y))*zz;}

float ex(float x, float y, float z){
 return y-0.5*x;
}

float ey ( float x, float y, float z ){
 return z-2*x;
}

void vectphi(float x0, float y0, float z0,
float x1, float y1, float z1,int mm){
float ex0, ex1, ey0, ey1;
int ix0, ix1, iy0, iy1;
     ex0=ex(x0,y0,z0);
     ix0=(ex0-exmin)*gmex/(exmax-exmin);
     ey0=ey(x0,y0,z0);
     iy0=(ey0-eymin)*gmey/(eymax-eymin);
     ex1=ex(x1,y1,z1);
     ix1=(ex1-exmin)*gmex/(exmax-exmin);
     ey1=ey(x1,y1,z1);
     iy1=(ey1-eymin)*gmey/(eymax-eymin);
     if (mm) sline(ix0,iy0,ix1,iy1);
      else line(ix0,gmey-iy0,ix1,gmey-iy1);
}
//---------------------------------------------------------------------------
__fastcall TForm1::TForm1(TComponent* Owner)
        : TForm(Owner){
int i, j;
float x,y,z;
  hy=(ymax-ymin)/ny;
  hx=(xmax-xmin)/nx;
  gmex=Form1->Image1->Width;
  gmey=Form1->Image1->Height;
  cosa=xv/sqrt(xv*xv+yv*yv);
  sina=yv/sqrt(xv*xv+yv*yv );
}
//---------------------------------------------------------------------------

void __fastcall TForm1::Button1Click(TObject *Sender){
zz+=0.1;
int i,j; float x, y, z;
  Form1->Image1->Canvas->FillRect(TRect(0,0,gmex,gmey));
  zmin=zmax=0.;
  for (i=0; i<=nx; i++)
  for (j=0; j<=ny; j++){
   z=fz(xmin+i*hx,ymin+j*hy);
   if (z>zmax) zmax=z;
   if (z<zmin) zmin=z;
}
 exmax=ex(xmin, ymax, zmax);
  exmin=ex(xmax, ymin, zmin);
  eymax=ey(xmin, ymin, zmax);
  eymin=ey(xmax, ymax, zmin);
  for(x=xmin; x<=xmax; x+=xmax-xmin)
  for(y=ymin; y<=ymax; y+=ymax-ymin)
  for(z=zmin; z<=zmax; z+=zmax-zmin){
        if (exmax<ex(x,y,z)) exmax=ex(x,y,z);
        if (exmin>ex(x,y,z)) exmin=ex(x,y,z);
        if (eymax<ey(x,y,z)) eymax=ey(x,y,z);
        if (eymin>ex(x,y,z)) eymin=ey(x,y,z);
  }
 phimax=new int[gmex]; phimin=new int[gmex];
    for(i=0;i<gmex;i++) {phimax[i]=0; phimin[i]=gmey;}
    cval=fz(xmax, ymax);
    for(i=ny-1;i>=0;i--){
        cvals[i+1]=cval; y=ymin+hy*i;
        cval=fz(xmax, y);
        vectphi(xmax, y+hy, cvals[i+1], xmax, y, cval, 1);
    }
    cvals[0] = cval ;
    for (j=nx-1;j>=0;j--){
        x=xmin+hx*j;
        cval=fz(x, ymax);
        vectphi(x+hx, ymax, cvals[ny], x,ymax,cval, 1);
        for(i=ny-1;i>=0;i--){
                cvals[i+1]=cval; y=ymin+hy*i;
              cval=fz(x, y);
                vectphi(x+hx, y, cvals[i], x, y, cval, 1);
                vectphi(x, y+hy, cvals[i+1], x, y, cval, 1);
        }
        cvals[0] = cval ;
    }
    vectphi(xmax, ymax, zmax, xmin, ymax, zmax, 0);
    vectphi(xmax, ymax, zmax, xmax, ymax, zmin, 0);
    vectphi(xmax, ymax, zmax, xmax, ymin, zmax, 0);
    vectphi(xmin, ymax, zmin, xmin, ymax, zmax, 0);
    vectphi(xmin, ymax, zmin, xmax, ymax, zmin, 0);
    vectphi(xmax, ymin, zmin, xmax, ymin, zmax, 0);
    vectphi(xmax, ymin, zmin, xmax, ymax, zmin, 0);
    vectphi(xmin, ymin, zmin, xmin, ymin, zmax, 1);
    vectphi(xmin, ymin, zmin, xmax, ymin, zmin, 1);
    vectphi(xmin, ymin, zmin, xmin, ymax, zmin, 1);
    vectphi(xmax, ymin, zmax, xmin, ymin, zmax, 1);
    vectphi(xmin, ymax, zmax, xmin, ymin, zmax, 1);
    delete phimax; delete phimin;
}

Программная реализация с использованием алгоритма плавающего горизонта показана на рисунке 1.

C++ Компьютерная графика

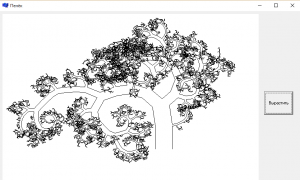
Построить дерево Аммерала

Задание
Построить дерево Аммерала.

В данной работе отражен вывод дерева Аммерала в среде программирования Borland С++ Builder 6 Enterprise. А так же разработка исходного кода вывода функции.

Пояснение. Идея алгоритма построения дерева принадлежит Аммералу. Сначала выводится прямоугольник, соответствующий стволу дерева. Затем на верхней стороне прямоугольника строится прямоугольный треугольник, для которого эта сторона служит гипотенузой. Затем на каждом из катетов полученного прямоугольного треугольника будут построены прямоугольники, и этот процесс будет рекурсивно применен к каждому из этих двух прямоугольников.

//---------------------------------------------------------------------------
#include <vcl.h>
#pragma hdrstop
#include <math.h>
#include "rgz2zd2.h"
//---------------------------------------------------------------------------
#pragma package(smart_init)
#pragma resource "*.dfm"
TForm1 *Form1;
//---------------------------------------------------------------------------
__fastcall TForm1::TForm1(TComponent* Owner)
        : TForm(Owner)
{
}
//---------------------------------------------------------------------------
float xmin=-400, xmax=800; // масштаб по x
float ymin=200, ymax=1300; //мастштаб по у
const double PI=3.14159;
int maxX, maxY, zz=0;
float xdens, ydens;
int ex(float x){
	return (int) ((x-xmin)/xdens);
}
int ey(float y){
	return (int) ((ymax-y)/ydens);
}
//вывод отрезка
void line(int x0, int y0,int x1, int y1){
        Form1->Image1->Canvas->MoveTo(x0,y0);
        Form1->Image1->Canvas->LineTo(x1,y1);
}

// рекурсивная функция построения дерева
void piphagor(float x0,float y0,float x1, float y1){
	float x0s, y0s, x1s, y1s, x2s, y2s;
	float lambda= 1.+(2.-1.)*(0.+rand()%10000)/10000;
	float phi= PI/2 + (PI-PI/2)*(0.+rand()%10000)/10000;
	if((x1-x0)*(x1-x0)+(y1-y0)*(y1-y0)<1){
			line(ex(x0),ey(maxY-y0),ex(x1),ey(maxY-y1));
			return;
	}
	x0s= x0-lambda*(y1-y0); y0s= y0+lambda*(x1-x0);
	x1s= x1-lambda*(y1-y0); y1s= y1+lambda*(x1-x0);
     	line(ex(x0), ey(maxY-y0), ex(x0s), ey(maxY-y0s));
	line(ex(x1), ey(maxY-y1), ex(x1s), ey(maxY-y1s));
	x2s= (x0s+x1s)/2+ (x1s-x0s)/2*cos(phi)-(y1s-y0s)/2*sin(phi);
	y2s= (y0s+y1s)/2+ (x1s-x0s)/2*sin(phi)+(y1s-y0s)/2*cos(phi);
	piphagor(x0s,y0s,x2s,y2s);
	piphagor(x2s,y2s,x1s,y1s);
}

void __fastcall TForm1::trolo(TObject *Sender){
Form1->Image1->Picture->Bitmap->FreeImage();
Form1->Image1->Picture->Bitmap = NULL;
maxX=Form1->Image1->Width;
maxY=Form1->Image1->Height;
xdens=(xmax-xmin)/maxX;
ydens=(ymax-ymin)/maxY;
piphagor(maxX/2+40, 0, maxX/2-40, 0);
}

Вывод построенного дерева показан на рисунке 1.

Компьютерная графика

Элементы диаграммы, которые используются для прогнозирования, — это:

линии тренда

Компьютерная графика

Элементарный фрагмент изображения на экране RGB монитора называется:

пиксел

Компьютерная графика

Элемент чертежа, обрабатываемый системой инженерной графики как целое, а не как совокупность точек или объектов, — это:

примитив

Компьютерная графика

Электронная таблица вывода результатов в системе STATISTICA — это:

Scrollsheet

Компьютерная графика

Шаблон пера в Си++ служит для:

рисования пунктирных и штрихпунктирных линий

Компьютерная графика

Чересстрочное появление предусмотрено в формате

GIF

Компьютерная графика

Чем больше экранное разрешение в цифровом видео, тем

больше четкость изображения

Компьютерная графика

Частота вертикальной развертки VSync, позволяющая получать на экране монитора устойчивое не мерцающее изображение, равна:

50-70 Гц